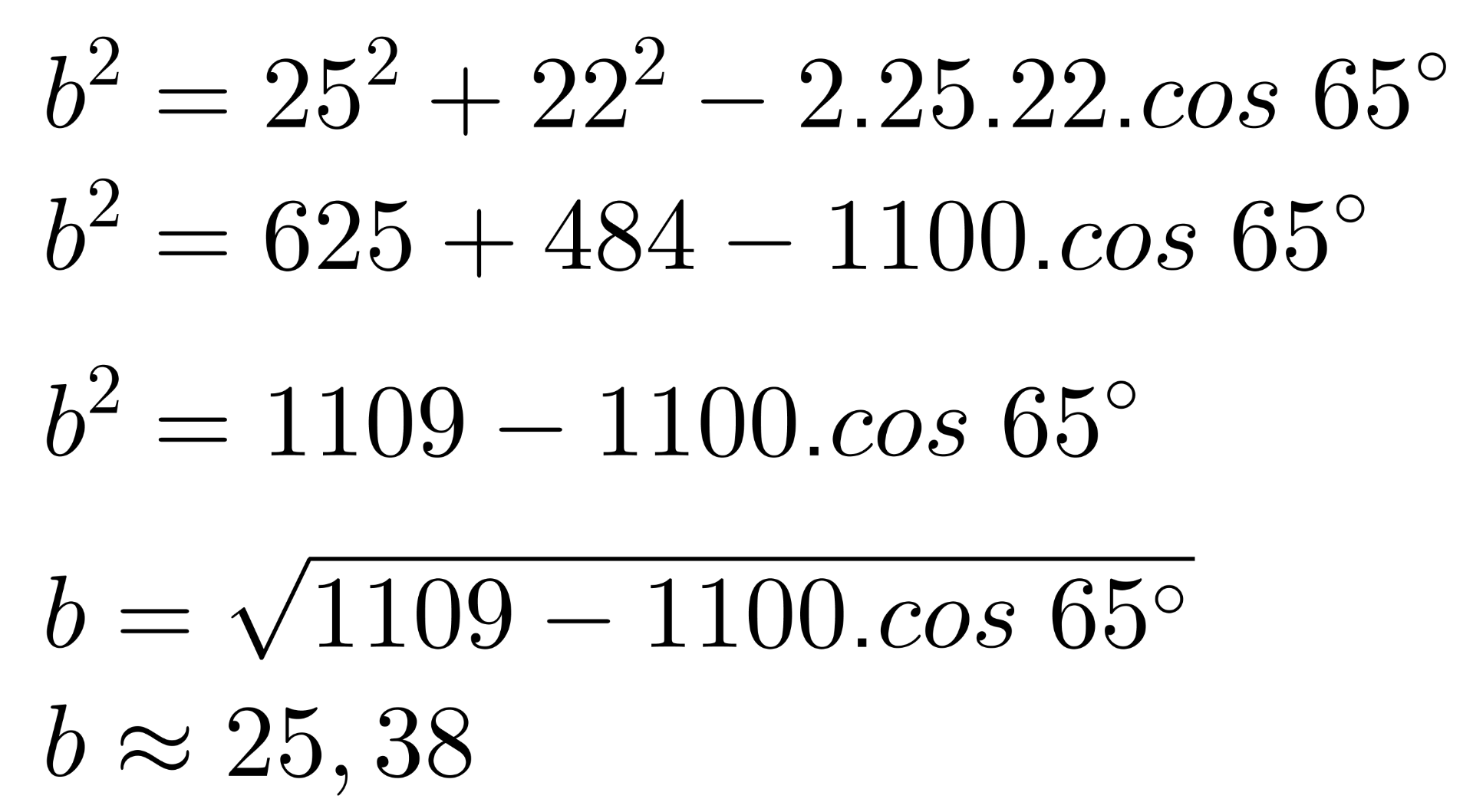Cuando trabajamos con triángulos no rectángulos, es decir oblicuángulos, para poder hallar los valores de sus lados o ángulos internos podremos aplicar dos teoremas, el teorema de seno y el teorema de coseno.
El teorema de seno y coseno son dos resultados que establecen las relaciones entre los ángulos interiores de cualquier triángulo con el seno y coseno de los lados opuestos a los ángulos.
Su aplicación permite conocer los ángulos o los lados del triángulo sin conocerlos todos.
Teorema de seno
En todo triángulo, las medidas de los lados son proporcionales a los senos de los respectivos ángulos opuestos.

Este teorema se aplica para averiguar las medidas de un triángulo conociendo:
- Dos ángulos y un lado, sabiendo a qué ángulo se opone.
- Dos lados y el ángulo opuesto a uno de ellos.
Veamos el siguiente ejemplo:
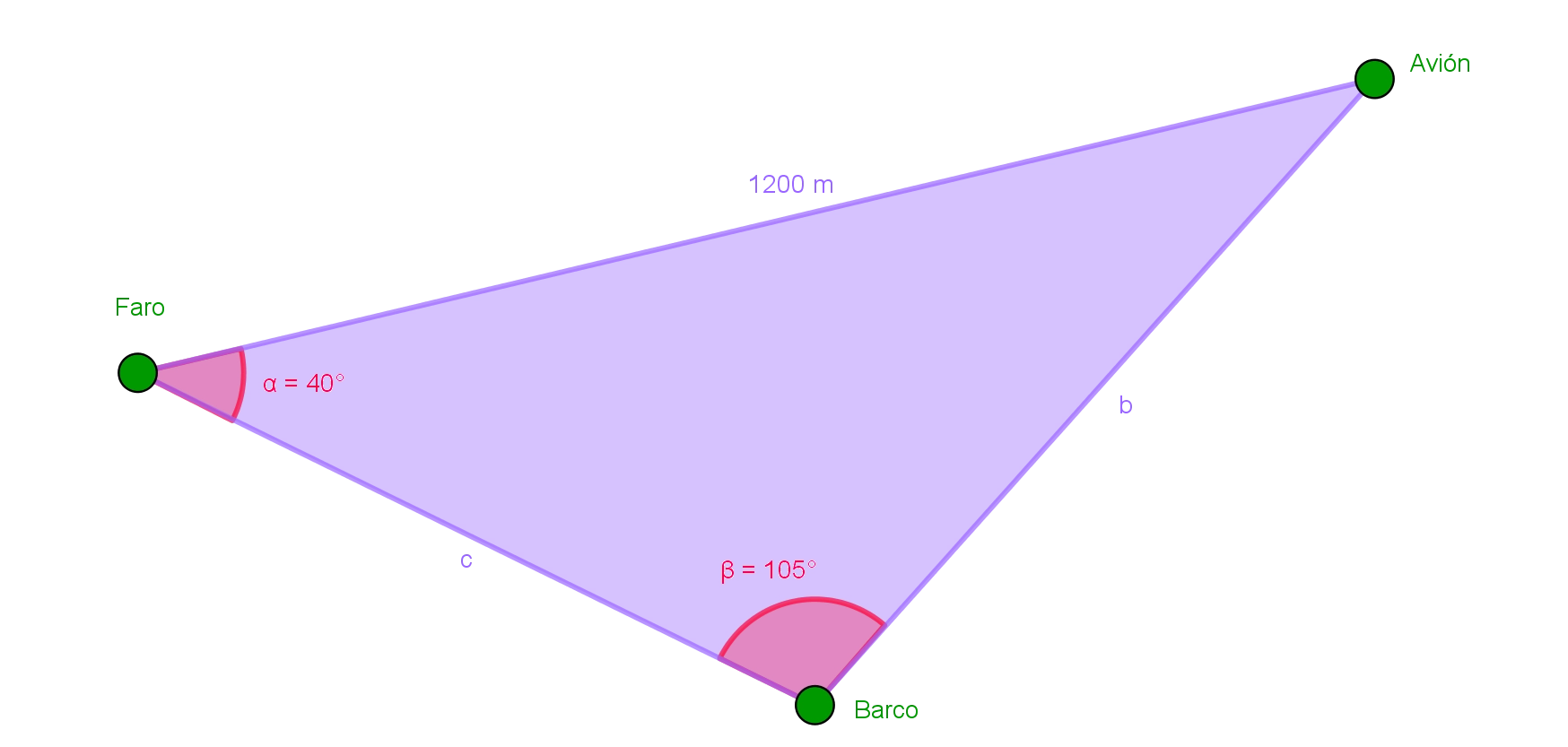
Desde lo alto de un faro se observa un avión que se encuentra a 1200 m de distancia y desde el mismo lugar se observa un barco. Sabiendo que el ángulo de observación entre el avión, el faro y el barco es de 40° y el ángulo que se forma entre el faro, el barco y el avión es de 105°. ¿Cuál es la distancia que hay del barco al avión y del barco al observador?


Teorema de coseno
En todo triángulo, el cuadrado de un lado es igual a la suma de los cuadrados de los otros dos menos el doble del producto de éstos por el coseno del ángulo comprendido entre ellos.

Este teorema se aplica para averiguar valores de un triángulo del que se conocen:*
- Dos lados y el ángulo comprendido entre ellos.
- Sus tres lados.
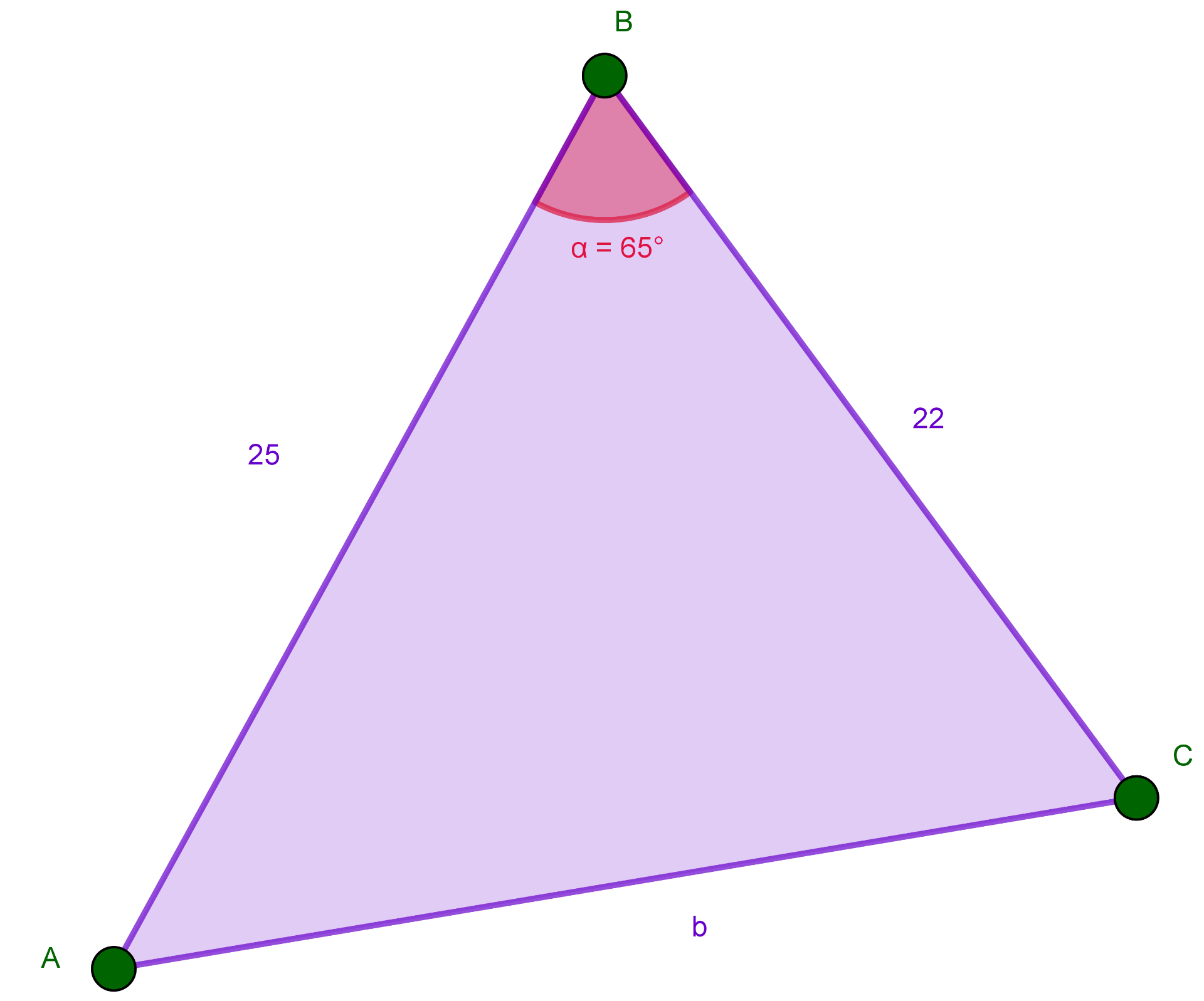
Tres amigas, Ana, Belén y Camila, van a una clase de yoga y se sientan formando un triángulo. Entre Ana y Belén hay 25 metros de distancia, entre Belén y Camila hay 12 metros y el ángulo que se forma en la esquina de Belén es de 65°, ¿Cuál es la distancia que hay entre Ana y Camila?