Estamos acostumbrados a multiplicar y dividir fracciones de manera mecánica sin comprender del todo el por qué obtenemos ese resultado, por lo cual hoy aprenderemos a multiplicar y dividir fracciones de manera gráfica.
Multiplicación de fracciones de manera gráfica


De manera similar multiplicaremos las fracciones, por ejemplo si deseamos multiplicar 3/4 x 2/5, primero representaremos de manera gráfica 3/4:

Aquí ya tenemos nuestras columnas, que están representadas por el primer factor. Para representar el segundo factor, en este caso 2/5 haremos lo mismo pero en vez de representarlo como columnas, lo representaremos como filas.

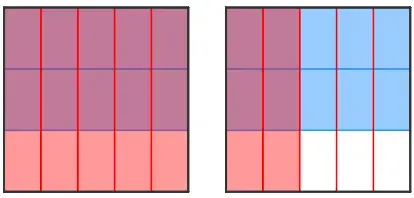
Para observar el resultado del producto de las fracciones mencionadas, debemos representar ambas fracciones en el mismo rectángulo, es decir, superponerlas, y la cantidad de cuadrados que tenga ambos colores será nuestro numerador mientras que la cantidad de cuadrados totales que queden formados por la cantidad de filas y columnas será nuestro denominador.

Como podemos observar, en total hay 20 cuadrados (entonces 20 será nuestro denominador) y de los 24 solo 6 comparten ambos colores por lo tanto, el resultado de 3/4×2/5 será 6/20.
También podemos resolverlo de manera analítica, multiplicando numerador por numerador y denominador por denominador y llegaremos al mismo resultado.
Juega con la siguiente animación y corrobora que se cumple, utiliza el deslizador «coloca uno encima del otro para poder desplazar las representaciones de fracciones.
¿Qué ocurre si el numerador es mayor que el denominador?

Al igual que antes, ahora representamos 2/3 pero en forma de filas:

Ahora solo nos queda superponer los cuadrados:

Primero contamos la cantidad de cuadrados que tienen ambos colores, en este caso son 14, ese será nuestro numerador.
Para indicar el denominador, tenemos en cuenta la cantidad de cuadrados que hay en un solo entero, ya que ambos tienen la misma cantidad. En este caso son 15 cuadrados, por lo tanto, 7/5×2/3=14/15 y si lo corroboramos analíticamente, llegaremos al mismo resultado.
División de fracciones de manera gráfica

Ahora que ya tenemos las dos fracciones con el mismo denominador, primero representaremos gráficamente la primera fracción, es decir 15/12:

Ahora veremos cuántas veces entra 8/12 en 15/12:

Como ambas tienen el mismo denominador, simplemente comparamos los numeradores y observamos cuántas veces entra 8 en 15.
Como podemos observar, 8 entra 1 vez y además tenemos 7 de los 8 rectángulos que necesitamos para formar el entero, por lo tanto la respuesta a la división 5/4:2/3 será 15/8 o 1 entero y 7/8. Podremos corroborarlo de manera analítica y llegaremos al mismo resultado.
Para repasar y seguir aprendiendo, continua en los siguientes enlaces: