Seguramente has tenido que estudiar los sistemas de ecuaciones lineales y has dicho… «¿para qué me sirve?«, «¿Por qué la tengo que estudiar?«, «Jamás la voy a usar«, entre otras célebres frases.
Hoy veremos distintas formas de aplicar lo aprendido y divertirte..
Ahora sí, comencemos…
Lo primero que tenemos que saber es de qué estamos hablando, para ello debemos aprender que un sistema de ecuaciones lineales es simplemente el encuentro de dos funciones lineales, los cuales pueden no encontrarse nunca, si son paralelas disjuntas, encontrarse una vez, si se cruzan, o tocarse infinitamente, si son coincidentes.
En otras palabras, podemos clasificar a los sistemas en 3 formas:
- Sistema compatible determinado (SCD): El sistema será compatible determinado cuando obtengamos una sola solución. Esta solución será en coordenadas, que puede ser (x;y) o (x;y;z) si trabajamos en 3 dimensiones. Obtendremos esta solución cuando las rectas se intercepten.
- Sistema compatible indeterminado (SCI): El sistema será compatible indeterminado cuando tengamos infinitas soluciones. Esto ocurre cuando las rectas son coincidentes, es decir, cuando querramos graficarlas, las mismas estarán posicionadas una encima de la otra.
- Sistema incompatible (SI): El sistema será incompatible cuando las rectas sean paralelas disjuntas, es decir cuando no se corten.
Pero… ¿Es posible divertirnos resolviendo sistemas de ecuaciones lineales?, veamos los siguientes problemas que comunmente se encuentran dispersos por internet:
Si quieres seguir practicando, haz clic en el siguiente enlace:



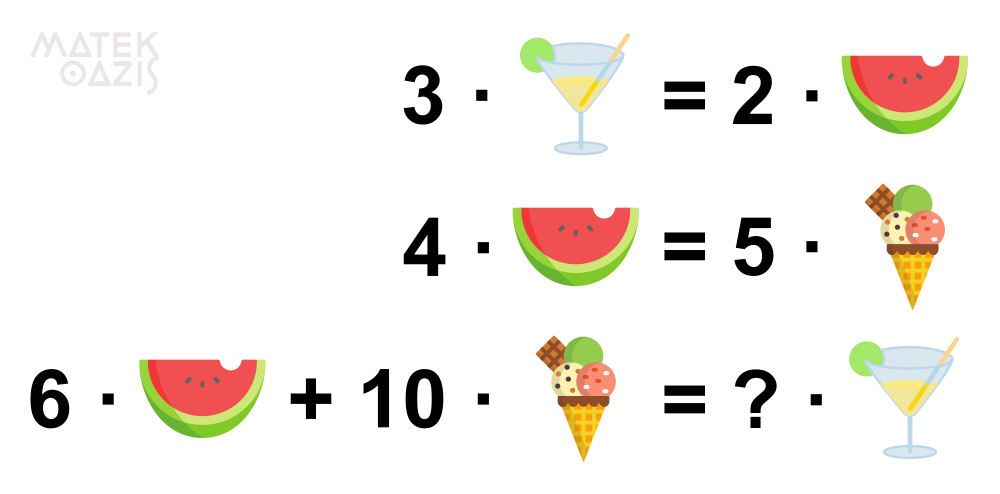
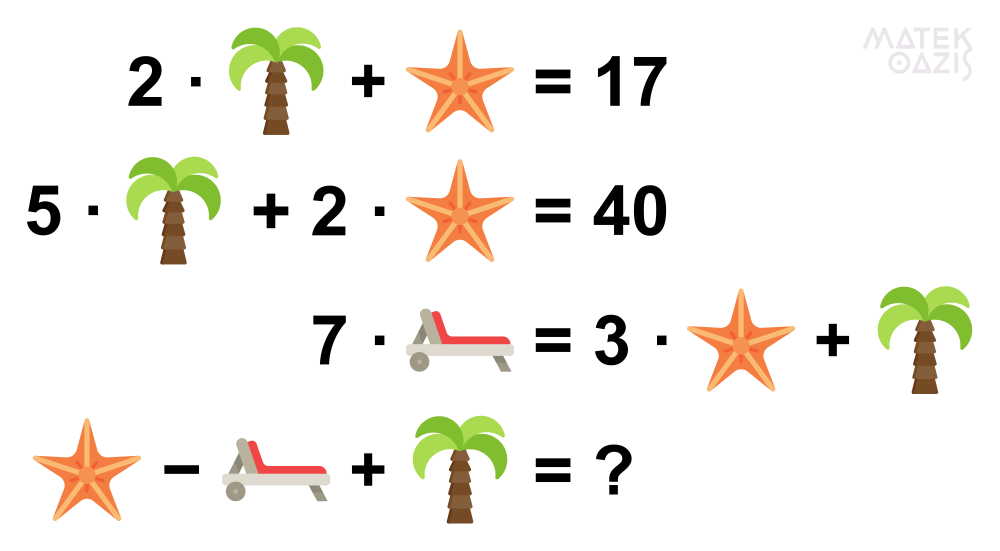
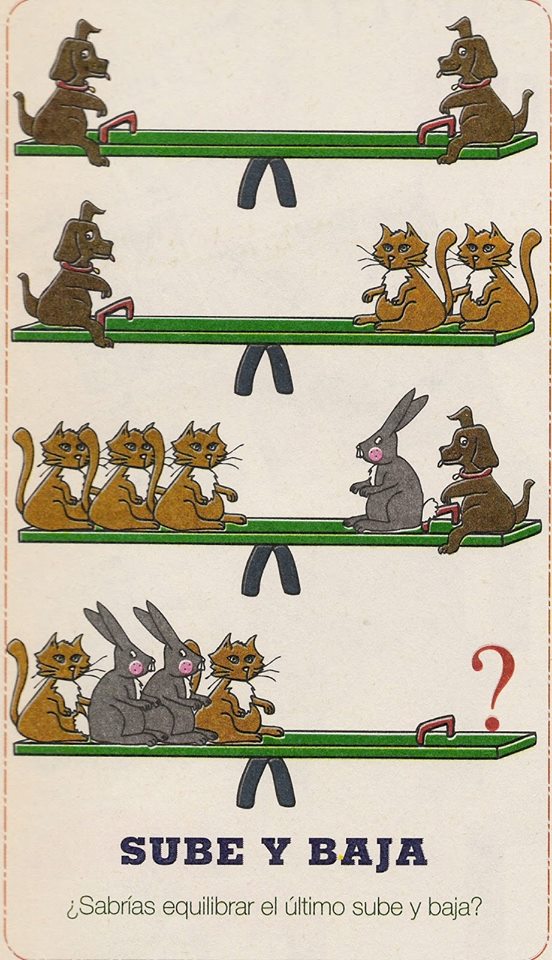
Veamos la primera imagen y cómo resolvera aplicando sistema de ecuaciones:

Primero debemos pensar a cada fruta como una incógnita, por lo cual la manzana será x, la pera y, y la palta z.
Ahora planteemos el problema como un sistema:

A simple vista podemos hallar el valor de las manzanas (x), que en este caso es 21. Reemplazando ese dato en las ecuaciones siguientes, obtenemos lo siguiente:

Ahora nos hace falta averiguar el valor de las peras (y) y de las paltas (z). Para ello podemos utilizar cualquiera de los métodos utilizados para resolver sistemas de ecuaciones. En este caso utilizaremos el método de sustitución, despejando en la primera ecuación, z y reemplazándola en la segunda ecuación:

Ahora solo nos queda resolver:

Ya tenemos el valor de las peras, que en este caso es 6. Por lo cual podremos obtener el valor de z simplemente reemplazando:
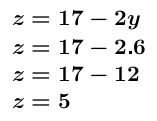
Para concluir solo nos queda resolver la última ecuación con los datos que tenemos:

Como puedes ver, hay distintas formas de divertirte al estudiar los sistemas de ecuaciones, te recomiendo seguir practicando con las imágenes que se encuentran más arriba.
Si quieres seguir practicando y divirtiéndote, te recomiendo el siguiente enlace:
