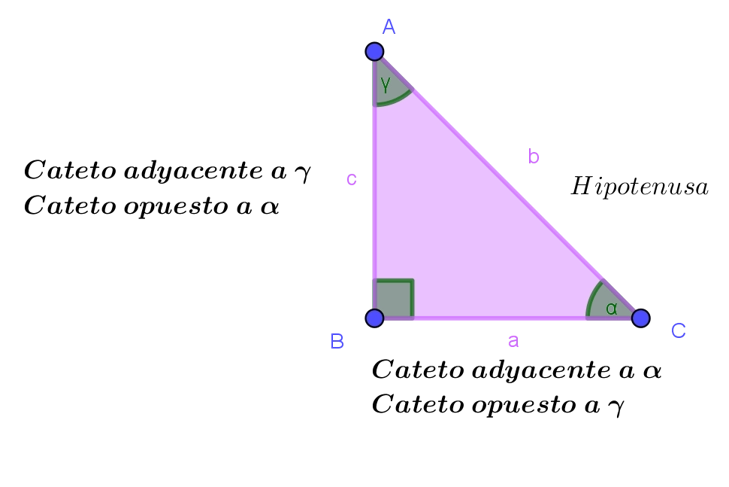
Para comprender las razones trigonométricas en un triángulo rectángulo, primero debemos saber identificar las relaciones que existen entre los elementos que componen un triángulo rectángulo.
•. Los ángulos agudos son complementarios: α+γ=90°
•La relación pitagórica: b^2=a^2+c^2
•Las razones trigonométricas.
En todo triángulo rectángulo se cumplen las siguientes razones trigonométricas:
Para poder recordar las tres razones trigonométricas principales (seno, coseno y tangente) puedes recordar la siguiente palabra:
Veamos un ejemplo:
Colocamos una escalera contra la pared con un ángulo de inclinación de 35° con el piso y la escalera mide 2,5 m, ¿a qué altura de la pared llegaremos?
Cálculo de un ángulo agudo a partir de dos lados
Para hallar la amplitud del ángulo agudo de un triángulo rectángulo si se conocen dos de sus lados, se debe utilizar la calculadora científica.
Por ejemplo:
Ángulos de elevación y depresión
Cuando observamos un objeto que no está a nuestra altura se forma un ángulo cuyos lados están definidos por dos líneas imaginarias: la línea horizontal, que pasa por nuestros ojos y la otra es la visual, que va de nuestros ojos al objeto.
Si se mira hacia arriba, el ángulo que forman ambas líneas imaginarias se llama «ángulo de elevación», caso contrario, «ángulo de depresión».

Veamos un ejemplo:
Un joven se acuesta sobre el pasto y observa la punta de un faro con un ángulo de elevación de 22°, si la distancia desde el joven hasta el faro es de 24 m, ¿cuál es la altura del faro?
Apliquemos sistema de ecuaciones
a. ¿A qué distancia del edificio se encuentra estacionado el vehículo?
b. ¿A qué altura de la calle se encuentra el primer balcón?
Veamos cómo quedaría representado gráficamente:
Para poder resolverlo, podemos ver que se forman dos triángulos rectángulos distintos por lo cual debemos comenzar a trabajar con los rectángulos por separado para poder construir el sistema de ecuaciones:
Ahora que ya tenemos los valores de x e y solo falta responder las dos preguntas:
a. El vehículo se encuentra aproximadamente a 13, 19 m.
b. Para saber la altura del primer balcón, debemos restarle 8 m al valor de x, por lo tanto el resultado será: 6,15 m.