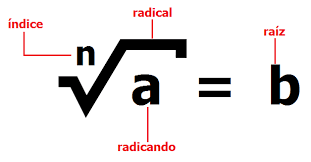
Hoy aprenderemos a operar con los radicales, es decir, con raíces. A continuación veremos las operaciones que podemos realizar:
- Simplificación y amplificación de radicales: Para poder simplificar o amplificar radicales, debemos seguir los siguientes pasos:
✓ Simplificación: Factorizamos el radicando y extraemos fuera de la raíz, todos los
términos posibles.

✓ Amplificación: Para poder amplificar un radical, debemos multiplicar tanto al índice
como al exponente del radicando por un mismo valor.

- Conversión de radicales a índice común (homogeneización): La homogeneización de radicales consiste en convertir los radicales de manera que tengan el mismo índice. Como por ejemplo:

Calculamos el mínimo común índice (se calcula de la misma manera que el mcm):

Amplificamos las raíces para que todas tengan índice 6:

- Adición y sustracción de radicales: Si los radicales son semejantes, sumamos o restamos los coeficientes y se escribe el mismo radical. Si no son semejantes, se intenta extraer factores para que lo sean. Si esto no es posible, se dejan indicados esos radicales. Veamos dos ejemplos:

- Multiplicación y división de radicales: Si los radicales son de igual índice, se multiplican o dividen los coeficientes y los radicandos por separado, y se mantiene el mismo índice. Si los radicales no son de igual índice, debemos homogeneizarlos. Veamos dos ejemplos:

- Racionalización de denominadores: La racionalización de denominadores consiste en hallar una fracción equivalente donde la raíz no se encuentre en el denominador, podemos hallar 3 casos de racionalización



¿Te gustaría jugar mientras aplicas las operaciones con radicales? Te invito a jugar el UNO RADICAL: