Movimientos en el plano

¿Te gustaría probar cómo varía la simetría?

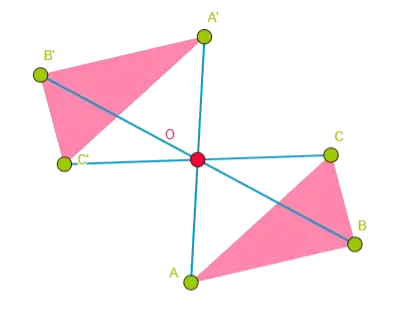
• Simetría central: es un tipo de simetría que se considera a partir de un punto que se conoce como centro de simetría. Todos los puntos correspondientes en una simetría central se denominan puntos homólogos y permiten trazar segmentos homólogos que son iguales y que disponen de ángulos correspondientes que también miden igual.

En otras palabras, en una simetría central, la imagen de un segmento es otro segmento con la misma longitud.

¿Cómo hallar la simetría central de un polígono?

Para hallar la simetría central de un polígono debemos seguir los siguientes pasos:

1. Al igual que en la simetría axial, en la central debemos marcar los vértices del polígono.
2. Tomamos el primer vértice y trazamos una recta que pase por el vértice y el centro de simetría.
3. Con ayuda del compás, medimos la distancia que hay entre el vértice y el centro de simetría y la trasladamos hacia el otro lado de la recta.
4. Volvemos a realizar el mismo procedimiento con los demás puntos.

¿Te gustaría probar cómo varía la simetría?

Rotación

También llamado giro, es un movimiento que se produce alrededor de un punto que mantiene la forma y el tamaño de la figura original.

La rotación está determinada por tres elementos:

• El ángulo que determina la amplitud de rotación.
• Un punto, llamado centro de rotación
• El sentido de la rotación, el cual puede ser negativo si rota en el mismo sentido de las agujas del reloj o positivo si rota al revés que las agujas del reloj.

¿Cómo rotamos un polígono?

Para rotar un polígono debemos seguir los siguientes pasos:

• Marcamos los vértices del polígono a rotar e identificar nuestro centro de rotación así como también el ángulo y el sentido de rotación.
• Unimos nuestro primer vértice con el centro de rotación y luego trazamos el ángulo de rotación y la recta que tendrá al vértice a rotar, dependiendo del sentido de rotación.
• Con la misma distancia que hay entre el centro y el vértice a trasladar, marcamos nuestro nuevo vértice en la recta trazada anteriormente.
• Repetimos el mismo procedimiento con los demás vértices, cuando hayamos terminado, unimos los vértices y podremos ver la figura rotada.

¿Te gustaría probar cómo varía la rotación?

Traslaciones

Como lo dice la palabra, la traslación es un movimiento en el plano donde se traslada un objeto a través de un vector.

¿Cómo trasladamos un polígono?

Al igual que en los otros movimientos, para poder trasladas un polígono tenemos que trasladar sus vértices y luego unir los vértices.

Para poder hacerlo, debemos transportar el vector que nos indicará el desplazamiento en cada uno de los vértices y, donde finaliza, allí se ubicará el vértice trasladado.

¿Te gustaría probar cómo varía la traslación?

Composición de movimientos

A una figura podemos realizarse diferentes movimientos sucesivos y esto forma una composición de movimientos.

Lo que debemos saber es que, en la composición de movimientos, para poder simbolizarlo debemos escribirlo en el orden inverso en el que se realizan, unidos por . Por ejemplo: